http://www.youtube.com/watch?v=_Pi8PW8vT2w&feature=youtu.be
postado por : Beatriz Mascarenhas
sexta-feira, 20 de dezembro de 2013
quinta-feira, 19 de dezembro de 2013
Questões sobre matrizes
Exercícios sobre Adição e Subtração de Matrizes
01 : Dadas as matrizes
 ,
,  e
e  , determine a matriz D resultante da operação A + B – C.
, determine a matriz D resultante da operação A + B – C.Resposta 01 :

02 : Os elementos de uma matriz M quadrada de ordem 3 x 3 são dados por aij, onde:
i + j, se i ≠ j
0, se i = j
Determine M + M.
Resposta 02 :

03 : (PUC–SP–Adaptada) São dadas as matrizes A = (aij) e B = (bij), quadradas de ordem 2, com aij = 3i + 4j e bij = – 4i – 3j. Considerando C = A + B, calcule a matriz C.
Resposta 03

04 : (PUCC–SP¬–Adaptada) Seja a matriz A = ( aij ) 2 x 2, em que aij = i + j, se i = j e i – j, se i ≠ j. Determine a matriz respeitando essas condições e calcule A + A + A.
Resposta 04:
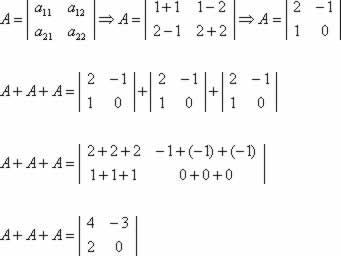
fonte: http://exercicios.brasilescola.com/matematica/exercicios-sobre-adicao-subtracao-matrizes.htm
postado por : Beatriz Mascarenhas
0, se i = j
Determine M + M.
Resposta 02 :

03 : (PUC–SP–Adaptada) São dadas as matrizes A = (aij) e B = (bij), quadradas de ordem 2, com aij = 3i + 4j e bij = – 4i – 3j. Considerando C = A + B, calcule a matriz C.
Resposta 03

04 : (PUCC–SP¬–Adaptada) Seja a matriz A = ( aij ) 2 x 2, em que aij = i + j, se i = j e i – j, se i ≠ j. Determine a matriz respeitando essas condições e calcule A + A + A.
Resposta 04:
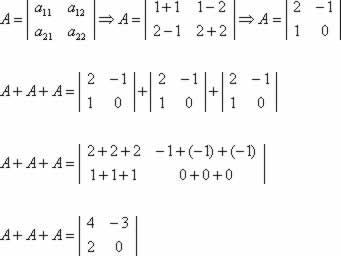
fonte: http://exercicios.brasilescola.com/matematica/exercicios-sobre-adicao-subtracao-matrizes.htm
postado por : Beatriz Mascarenhas
Paginá 102 do livro
5. |2 5| 2x-4= -8
|-1 -4|
6. |3 6| 3x10 = 30 6x2= 12 30-12 = 18
|2 10|
Postado por : Beatriz Mascarenhas
quarta-feira, 18 de dezembro de 2013
Paginá 110 . questão 32
- 32 . a) |6 5| |2 4| = |6.2 + 5.1 6.4 + 5.3| = |17 39|
|1 0| |1 3| |1.2 + 0.1 1.4 + 0.3| |2 4|
b) | 1 | |2 5 0 | 1x3 = |1.2 1.5 1.0| |2 5 0|
| 3 | |3.2 3.5 3.0| = |6 15 0|
| 6 | 3x1 |6.2 6.5 6.0| 3x3 |12 30 0|
c) |2 5 0| |1|
|3| = | 2.1 + 5.3 + 0.6 | = |17|
|6|
d) |1 3 6| |5 0| |1.5 + 3.2 + 6.3 1.0+ 3.4 +6.2|
|2 5 1| |2 4| = |2.5 + 5.2 + 1.3 2.0+ 5.4+1.2|
|4 0 2| |3 2| |4.5 + 0.2 + 2.3 4.0 +0.4+ 2.2|
| 2 24 9 27 |
| 4 13 11 12 |
por: Beatriz Mascarenhas
Exercicios sobre determinantes!
Vamos resolver algumas questões !
Pag 124
1.0 -Calcule os determinantes :
a - | 6 4|
|2 3 | = 6.3-4.2 = 18-8=10
B - | -3 -8
| 1 2|= (-3).2 - (-8).1 = -6+8 = 2
C- |6 10|
|3 5| = 6.5-101.3 = 30-30 = 0
D - | a a +1|
| b b+1| = a . (b+1) - ab +1 =
A - B
F- | a b |
| a+b a +b | = a .( a.b) - (a +b) .b = a² - b²
G - | sen x cos x |
| - seny cosy | = senx.cosy- cosy. ( -sen y ) = SEN X+Y
H- | cos a sen b|
| sen B cos A | = cos² = a +b=
cos² a - sen²b
2. Sendo A | 1 3 |
| 0 2 | e B = | -1 3|
|2 0| , calcule det AB
Det A = 1.2-0.3 = 2-0= 2
Det B = (-1).0- (2.3)= 6
3 . Dada A = | 1 0|
|2 4 | , calcule A ¹
1.0-2.4= 8
4 . Dadas as matrizes A=5 , B | (1) 2| ,| 3 -5 | C= 2 -2 |
|3 0 | calcule :
A.) DET A = 5
B) DET B= (-1).(-5)-3.2= -1
C) DET C = 2.0-3.(-2) = 0-6 = 6
D) DET A - DET B= 5- (-1) = 6
E) DET B . DET C = 1 . (-6) = -6
F ) DET ( B-C)= -1- ( +6)= 7
H) 2.DET B = 2.(-1)= -2
I ) DET ( AB) = DET ( 5-(-1)= -4
Postado por : Paloma Alves
Pag 124
1.0 -Calcule os determinantes :
a - | 6 4|
|2 3 | = 6.3-4.2 = 18-8=10
B - | -3 -8
| 1 2|= (-3).2 - (-8).1 = -6+8 = 2
C- |6 10|
|3 5| = 6.5-101.3 = 30-30 = 0
D - | a a +1|
| b b+1| = a . (b+1) - ab +1 =
A - B
F- | a b |
| a+b a +b | = a .( a.b) - (a +b) .b = a² - b²
G - | sen x cos x |
| - seny cosy | = senx.cosy- cosy. ( -sen y ) = SEN X+Y
H- | cos a sen b|
| sen B cos A | = cos² = a +b=
cos² a - sen²b
2. Sendo A | 1 3 |
| 0 2 | e B = | -1 3|
|2 0| , calcule det AB
Det A = 1.2-0.3 = 2-0= 2
Det B = (-1).0- (2.3)= 6
3 . Dada A = | 1 0|
|2 4 | , calcule A ¹
1.0-2.4= 8
4 . Dadas as matrizes A=5 , B | (1) 2| ,| 3 -5 | C= 2 -2 |
|3 0 | calcule :
A.) DET A = 5
B) DET B= (-1).(-5)-3.2= -1
C) DET C = 2.0-3.(-2) = 0-6 = 6
D) DET A - DET B= 5- (-1) = 6
E) DET B . DET C = 1 . (-6) = -6
F ) DET ( B-C)= -1- ( +6)= 7
H) 2.DET B = 2.(-1)= -2
I ) DET ( AB) = DET ( 5-(-1)= -4
Postado por : Paloma Alves
Aula video com Lara serra
CONTINUAÇÃO
-Matriz Triangular
-Matriz Diagonal
-Matriz Identidade
-Matriz Nula
-Matriz Triangular
-Matriz Diagonal
-Matriz Identidade
-Matriz Nula
segunda-feira, 16 de dezembro de 2013
Exercicios sobre determinantes !
Vamos resolver alguns exercicios :
U.F. Ouro Preto – MG
1.0 ) Considere a matriz:


Ao resolver esta desigualdade obteremos o seguinte conjunto solução:


2.0 -
Seja a um número real e seja:

a) Para a=1, encontre todas as raízes da equação p(x)=0
b) Encontre os valores de a para os quais a equação p(x)=0 tem uma única raiz real.
Solução :
Postado por : Paloma Alves
1.0 ) Considere a matriz:


Ao resolver esta desigualdade obteremos o seguinte conjunto solução:


2.0 -
Seja a um número real e seja:

a) Para a=1, encontre todas as raízes da equação p(x)=0
b) Encontre os valores de a para os quais a equação p(x)=0 tem uma única raiz real.
Solução :
a) Façamos o determinante com o valor de a = 1:

Temos o produto de duas parcelas igual a zero, então teremos duas situações:
3 - x = 0 ou (1 - x) 2 + 4 = 0
Na primeira temos que x = 3; na segunda não é possível determinar uma solução.
Logo, temos apenas uma raiz possível quando a for igual a 1.
b)

Novamente teremos duas situações: uma onde x=3 e a outra temos que determinar para quais valores de a teremos apenas a solução x = 3:

Para que só exista uma única raiz, essa equação do segundo grau não deve ter raiz, ou seja, seu discriminante deve ser menor que zero.



Temos o produto de duas parcelas igual a zero, então teremos duas situações:
3 - x = 0 ou (1 - x) 2 + 4 = 0
Na primeira temos que x = 3; na segunda não é possível determinar uma solução.
Logo, temos apenas uma raiz possível quando a for igual a 1.
b)

Novamente teremos duas situações: uma onde x=3 e a outra temos que determinar para quais valores de a teremos apenas a solução x = 3:

Para que só exista uma única raiz, essa equação do segundo grau não deve ter raiz, ou seja, seu discriminante deve ser menor que zero.


Postado por : Paloma Alves
Me salva ! Determinante de ordem 3
Determinantes de 3 ordem, regra de Sarrus :
Tirem suas grandes dúvidas, e depois vejamos alguns exercícios do livro .
Postado por : Paloma Alves e Lara Serra
Fonte : http://www.youtube.com/watch?v=zp7726v2sfo
Tirem suas grandes dúvidas, e depois vejamos alguns exercícios do livro .
Postado por : Paloma Alves e Lara Serra
Fonte : http://www.youtube.com/watch?v=zp7726v2sfo
Me salva ! Determinante de ordem 1
Alguns pesam que isso é uma dor de cabeça ,mais se parar pra raciocinar vai vê que nem é tão dificil.
Vamos lá então aprender mais um pouco ?
Qualquer coisa tirar dúvidas com o professor, :)
Postado por : Paloma Alves
Fonte : http://www.youtube.com/watch?v=xbIPs545xAQ
Vamos lá então aprender mais um pouco ?
Qualquer coisa tirar dúvidas com o professor, :)
Postado por : Paloma Alves
Fonte : http://www.youtube.com/watch?v=xbIPs545xAQ
Videos sobre determinantes !
Vejamos a seguir, um pouco da aula sobre determinante :
http://www.youtube.com/watch?v=KW-ttTTObhY
Postado por : Paloma Alves
Fonte : http://www.youtube.com/watch?v=KW-ttTTObhY
http://www.youtube.com/watch?v=KW-ttTTObhY
Postado por : Paloma Alves
Fonte : http://www.youtube.com/watch?v=KW-ttTTObhY
Determinantes
Vejamos o conceito de determinantes :

DetA = 12 + 9
DetA = 21
Como já vimos, matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou seja, é do tipo nxn).
Determinante de 2ª ordem
Dada a matriz ,
de ordem 2, por definição o determinante associado a M, determinante de
2ª ordem, é dado por:
,
de ordem 2, por definição o determinante associado a M, determinante de
2ª ordem, é dado por:
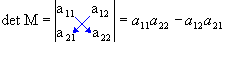
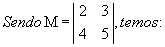
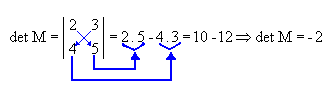
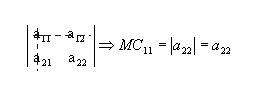
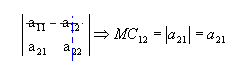
O determinante de uma Matriz é dado pelo
valor numérico resultante da subtração entre o somatório do produto dos
termos da diagonal principal e do somatório do produto dos termos da
diagonal secundária. Nas matrizes quadradas de ordem 3x3 esses cálculos
podem ser efetuados repetindo-se a 1ª e a 2ª coluna, aplicando em
seguida a regra de Sarrus. Lembrando que uma matriz é quadrada quando o
número de linhas é igual ao número de colunas.
Observe o cálculo de determinantes nas seguintes matizes quadradas de ordem 2x2 e 3x3:
Observe o cálculo de determinantes nas seguintes matizes quadradas de ordem 2x2 e 3x3:
Determinante de uma matriz A de ordem 2 x 2.

Diagonal principal: 2 * 6 = 12
Diagonal secundária: 9 * (–1) = – 9
DetA = 12 – (–9)Diagonal secundária: 9 * (–1) = – 9
DetA = 12 + 9
DetA = 21
Como já vimos, matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou seja, é do tipo nxn).
A toda matriz
quadrada está associado um número ao qual damos o nome de determinante.
Dentre as
várias aplicações dos determinantes na Matemática, temos:
-
resolução de alguns tipos de sistemas de equações lineares;
-
cálculo da área de um triângulo situado no plano cartesiano, quando são conhecidas as coordenadas dos seus vértices;
Determinante de
1ª ordem
Dada uma matriz
quadrada de 1ª ordem M=[a11], o seu determinante é o número real a11:
det M =Ia11I = a11
Observação: Representamos o
determinante de uma matriz entre duas barras verticais, que não têm o
significado de módulo.
Por exemplo:
|
|
Determinante de 2ª ordem
Dada a matriz
 ,
de ordem 2, por definição o determinante associado a M, determinante de
2ª ordem, é dado por:
,
de ordem 2, por definição o determinante associado a M, determinante de
2ª ordem, é dado por: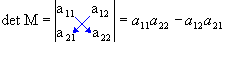
Portanto, o determinante
de uma matriz de ordem 2 é dado pela diferença entre o produto dos elementos
da diagonal principal e o produto dos elementos da diagonal secundária. Veja o
exemplo a seguir.
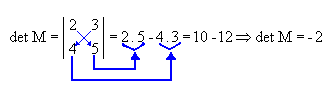
Menor
complementar
Chamamos de menor
complementar relativo a um elemento aij de uma
matriz M, quadrada e de ordem n>1, o determinante MCij ,
de ordem n - 1, associado à matriz obtida de M quando suprimimos a linha
e a coluna que passam por aij .
Vejamos como
determiná-lo pelos exemplos a seguir:
a) Dada a matriz  ,
de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11),
retiramos a linha 1 e a coluna 1:
,
de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11),
retiramos a linha 1 e a coluna 1:
 ,
de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11),
retiramos a linha 1 e a coluna 1:
,
de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11),
retiramos a linha 1 e a coluna 1: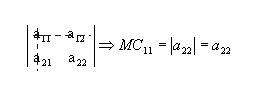
Da mesma forma, o menor complementar relativo
ao elemento a12 é:
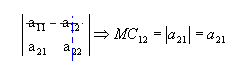
b) Sendo  ,
de ordem 3, temos:
,
de ordem 3, temos:
 ,
de ordem 3, temos:
,
de ordem 3, temos:
|
Matriz quadrada ( videos )
Vejamos um pouco mais sobre matriz quadrada , veja a seguir :
Postado por : Paloma Alves
Fonte : http://www.youtube.com/watch?v=4YyMJ4qriRc
Postado por : Paloma Alves
Fonte : http://www.youtube.com/watch?v=4YyMJ4qriRc
Tipos de Matrizes vejamos passo a passo!
Caractéristicas de matrizes : Algumas matrizes recebem os nomes especias :
A. Matriz Linha
A. Matriz Linha
É a matriz que possui uma única linha.
Exemplos
1) A = [–1, 0]
2) B=[1 0 0 2]
B. Matriz Coluna





B. Matriz Coluna
É a matriz que possui uma única coluna.
Exemplos

C. Matriz Nula
É a matriz que possui todos os elementos iguais a zero.
Exemplos
D.
Matriz Quadrada
É a matriz que possui o número de linhas igual ao número de colunas.
Exemplos

Observações:
1ª) Quando uma matriz não é quadrada, ela é chamada de retangular.
2ª) Dada uma matriz quadrada de ordem n, chamamos de diagonal principal da matriz ao conjunto dos elementos que possuem índices iguais.
Exemplo

{a11, a22, a33, a44} é a diagonal principal da matriz A.
3ª) Dada a matriz quadrada de ordem n, chamamos de diagonal secundária da matriz ao conjunto dos elementos que possuem a soma dos dois índices igual a n + 1.
Exemplo:

{a14, a23, a32, a41} é a diagonal secundária da matriz A.
Vejamos a seguir ,alguns videos .
Postado por : Paloma Alves
Fonte : http://pt.wikipedia.org/wiki/Matriz_%28matem%C3%A1tica%29
Operações com Matrizes (Adiçao, subtração)
Adição
Para adicionarmos duas ou mais matrizes é preciso que todas elas tenham o mesmo número de linhas e de colunas. A soma dessas matrizes irá resultar em outra matriz que também terá o mesmo número de linhas e de colunas.
Os termos deverão ser somados com os seus termos correspondentes.
Concluímos que:
Dada duas matrizes, A e B, as duas de ordem m x n. Então, A + B = C, com
C de ordem m x n ↔ a11 + b11 = c11.
Veja o exemplo abaixo:
Dado a matriz A =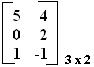 e matriz B =
e matriz B = 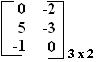 , se efetuarmos a soma dessas matrizes teremos:
, se efetuarmos a soma dessas matrizes teremos:
Somaremos os termos correspondentes em cada matriz:
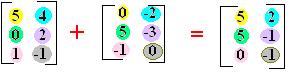
Subtração
Para efetuarmos a subtração de duas matrizes, as matrizes subtraídas devem ter a mesma ordem (mesmo número de linhas e colunas) e a matriz obtida com a subtração (matriz diferença) também deve ter o mesmo número de linhas e colunas que as matrizes subtraídas.
Cada elemento de uma matriz deve ser subtraído com o elemento correspondente da outra matriz.
Concluímos que:
Dada duas matrizes, A e B, as duas de ordem m x n. Então A – B = C de
ordem m x n ↔ a11 – a11 = c11
Veja o exemplo abaixo:
Dada a matriz A = 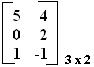 e a matriz B =
e a matriz B = 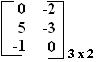 , se efetuamos a subtração dessas matrizes, temos:
, se efetuamos a subtração dessas matrizes, temos:
Subtraindo os termos correspondentes das matrizes:
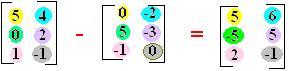
Com a subtração das duas matrizes obtivemos uma matriz C = 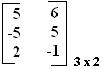
Com a soma das duas matrizes obtivemos outra matriz C =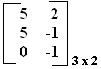 .
.
Postado por :LARA SERRA
Matriz 2
O que vem a ser Matriz ? Vamos saber um pouco mais :
Uma matriz MxN é uma tabela M DE LINHAS e N DE COLUNAS sobre um conjunto ,normalmente um corpo F representada sobre a forma de um quadro.As matrizes são muito utilizadas para a resolução de sistemas de equações lineares e transformações lineares.
As linhas horizontais da matriz são chamadas de linhas e as linhas verticais são chamadas de colunas. Logo uma matriz com
 linhas e
linhas e  colunas é chamada de uma matriz
colunas é chamada de uma matriz  por
por  (escreve-se
(escreve-se  ) e
) e  e
e  são chamadas de suas dimensões, tipo ou ordem. Por exemplo, a matriz a seguir é uma matriz de ordem
são chamadas de suas dimensões, tipo ou ordem. Por exemplo, a matriz a seguir é uma matriz de ordem 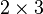 com elementos naturais.
com elementos naturais. Um elemento de uma matriz
Um elemento de uma matriz  que está na
que está na  -ésima linha e na
-ésima linha e na  -ésima coluna é chamado de elemento
-ésima coluna é chamado de elemento  ou
ou 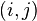 -ésimo elemento de
-ésimo elemento de 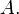 Ele é escrito como
Ele é escrito como 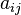 ou
ou ![a[i,j]](http://upload.wikimedia.org/math/9/1/9/919d3c090a103264561de7072f1ac629.png) . Nesse exemplo, o elemento
. Nesse exemplo, o elemento  é
é  , o número na primeira linha e segunda coluna do quadro.
, o número na primeira linha e segunda coluna do quadro.
- Existe várias matrizes,podemos observar :
- Matriz Linha
- Matriz Nula
- Matriz Quadrada
- Matriz Triangular
- Matriz Diagonal
- Matriz identidade
- Subtração de Matrizes
- Adição de Matrizes
- Multiplicação de Matrizes
- Matriz transposta
- Matriz Inversa
- Aplicações de Matrizes
- Postado por : Paloma Brito Alves
Fonte : http://www.vestibulandoweb.com.br/matematica/teoria/tipos-de-matrizes.asp
Subscrever:
Comentários (Atom)