http://www.youtube.com/watch?v=_Pi8PW8vT2w&feature=youtu.be
postado por : Beatriz Mascarenhas
Matematica nota 100
sexta-feira, 20 de dezembro de 2013
quinta-feira, 19 de dezembro de 2013
Questões sobre matrizes
Exercícios sobre Adição e Subtração de Matrizes
01 : Dadas as matrizes
 ,
,  e
e  , determine a matriz D resultante da operação A + B – C.
, determine a matriz D resultante da operação A + B – C.Resposta 01 :

02 : Os elementos de uma matriz M quadrada de ordem 3 x 3 são dados por aij, onde:
i + j, se i ≠ j
0, se i = j
Determine M + M.
Resposta 02 :

03 : (PUC–SP–Adaptada) São dadas as matrizes A = (aij) e B = (bij), quadradas de ordem 2, com aij = 3i + 4j e bij = – 4i – 3j. Considerando C = A + B, calcule a matriz C.
Resposta 03

04 : (PUCC–SP¬–Adaptada) Seja a matriz A = ( aij ) 2 x 2, em que aij = i + j, se i = j e i – j, se i ≠ j. Determine a matriz respeitando essas condições e calcule A + A + A.
Resposta 04:
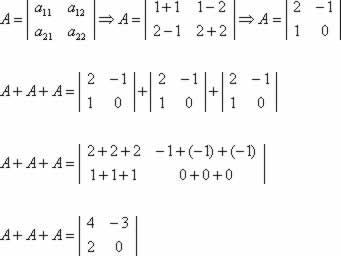
fonte: http://exercicios.brasilescola.com/matematica/exercicios-sobre-adicao-subtracao-matrizes.htm
postado por : Beatriz Mascarenhas
0, se i = j
Determine M + M.
Resposta 02 :

03 : (PUC–SP–Adaptada) São dadas as matrizes A = (aij) e B = (bij), quadradas de ordem 2, com aij = 3i + 4j e bij = – 4i – 3j. Considerando C = A + B, calcule a matriz C.
Resposta 03

04 : (PUCC–SP¬–Adaptada) Seja a matriz A = ( aij ) 2 x 2, em que aij = i + j, se i = j e i – j, se i ≠ j. Determine a matriz respeitando essas condições e calcule A + A + A.
Resposta 04:
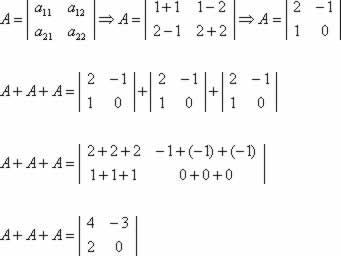
fonte: http://exercicios.brasilescola.com/matematica/exercicios-sobre-adicao-subtracao-matrizes.htm
postado por : Beatriz Mascarenhas
Paginá 102 do livro
5. |2 5| 2x-4= -8
|-1 -4|
6. |3 6| 3x10 = 30 6x2= 12 30-12 = 18
|2 10|
Postado por : Beatriz Mascarenhas
quarta-feira, 18 de dezembro de 2013
Paginá 110 . questão 32
- 32 . a) |6 5| |2 4| = |6.2 + 5.1 6.4 + 5.3| = |17 39|
|1 0| |1 3| |1.2 + 0.1 1.4 + 0.3| |2 4|
b) | 1 | |2 5 0 | 1x3 = |1.2 1.5 1.0| |2 5 0|
| 3 | |3.2 3.5 3.0| = |6 15 0|
| 6 | 3x1 |6.2 6.5 6.0| 3x3 |12 30 0|
c) |2 5 0| |1|
|3| = | 2.1 + 5.3 + 0.6 | = |17|
|6|
d) |1 3 6| |5 0| |1.5 + 3.2 + 6.3 1.0+ 3.4 +6.2|
|2 5 1| |2 4| = |2.5 + 5.2 + 1.3 2.0+ 5.4+1.2|
|4 0 2| |3 2| |4.5 + 0.2 + 2.3 4.0 +0.4+ 2.2|
| 2 24 9 27 |
| 4 13 11 12 |
por: Beatriz Mascarenhas
Exercicios sobre determinantes!
Vamos resolver algumas questões !
Pag 124
1.0 -Calcule os determinantes :
a - | 6 4|
|2 3 | = 6.3-4.2 = 18-8=10
B - | -3 -8
| 1 2|= (-3).2 - (-8).1 = -6+8 = 2
C- |6 10|
|3 5| = 6.5-101.3 = 30-30 = 0
D - | a a +1|
| b b+1| = a . (b+1) - ab +1 =
A - B
F- | a b |
| a+b a +b | = a .( a.b) - (a +b) .b = a² - b²
G - | sen x cos x |
| - seny cosy | = senx.cosy- cosy. ( -sen y ) = SEN X+Y
H- | cos a sen b|
| sen B cos A | = cos² = a +b=
cos² a - sen²b
2. Sendo A | 1 3 |
| 0 2 | e B = | -1 3|
|2 0| , calcule det AB
Det A = 1.2-0.3 = 2-0= 2
Det B = (-1).0- (2.3)= 6
3 . Dada A = | 1 0|
|2 4 | , calcule A ¹
1.0-2.4= 8
4 . Dadas as matrizes A=5 , B | (1) 2| ,| 3 -5 | C= 2 -2 |
|3 0 | calcule :
A.) DET A = 5
B) DET B= (-1).(-5)-3.2= -1
C) DET C = 2.0-3.(-2) = 0-6 = 6
D) DET A - DET B= 5- (-1) = 6
E) DET B . DET C = 1 . (-6) = -6
F ) DET ( B-C)= -1- ( +6)= 7
H) 2.DET B = 2.(-1)= -2
I ) DET ( AB) = DET ( 5-(-1)= -4
Postado por : Paloma Alves
Pag 124
1.0 -Calcule os determinantes :
a - | 6 4|
|2 3 | = 6.3-4.2 = 18-8=10
B - | -3 -8
| 1 2|= (-3).2 - (-8).1 = -6+8 = 2
C- |6 10|
|3 5| = 6.5-101.3 = 30-30 = 0
D - | a a +1|
| b b+1| = a . (b+1) - ab +1 =
A - B
F- | a b |
| a+b a +b | = a .( a.b) - (a +b) .b = a² - b²
G - | sen x cos x |
| - seny cosy | = senx.cosy- cosy. ( -sen y ) = SEN X+Y
H- | cos a sen b|
| sen B cos A | = cos² = a +b=
cos² a - sen²b
2. Sendo A | 1 3 |
| 0 2 | e B = | -1 3|
|2 0| , calcule det AB
Det A = 1.2-0.3 = 2-0= 2
Det B = (-1).0- (2.3)= 6
3 . Dada A = | 1 0|
|2 4 | , calcule A ¹
1.0-2.4= 8
4 . Dadas as matrizes A=5 , B | (1) 2| ,| 3 -5 | C= 2 -2 |
|3 0 | calcule :
A.) DET A = 5
B) DET B= (-1).(-5)-3.2= -1
C) DET C = 2.0-3.(-2) = 0-6 = 6
D) DET A - DET B= 5- (-1) = 6
E) DET B . DET C = 1 . (-6) = -6
F ) DET ( B-C)= -1- ( +6)= 7
H) 2.DET B = 2.(-1)= -2
I ) DET ( AB) = DET ( 5-(-1)= -4
Postado por : Paloma Alves
Aula video com Lara serra
CONTINUAÇÃO
-Matriz Triangular
-Matriz Diagonal
-Matriz Identidade
-Matriz Nula
-Matriz Triangular
-Matriz Diagonal
-Matriz Identidade
-Matriz Nula
Subscrever:
Comentários (Atom)

